티스토리 뷰

0. 서론
Competitive Programming(이하 CP)을 공부하는 분들에게 기하는 큰 골칫거리입니다. ICPC나 Codeforces에 무시하지 못할 만큼 출제되면서 동시에 기하에 대한 양질의 정보가 부족한 것이 이유라고 생각하고 있습니다. 그래서 이번 기회에 기하 문제를 편하게 풀기 위한 많은 정보와 팁을 정리하려고 합니다. 이 글을 통해 많은 분들이 기하를 까다롭게 느끼지 않았으면 좋겠습니다.
제가 조사한 기하가 어려운 이유는 다음과 같습니다.
- 대부분의 문제가 실수 오차에 매우 민감하다.
- 예외 처리할 것이 매우 많다.
- 코딩을 깔끔하게 하기 어렵다.
- 다른 분야와 공유하는 부분이 없어 생소하다.
이 글의 목표는 위의 이유들을 해결하는 것입니다. 제 글을 통해 여러분이 더 이상 기하를 까다롭다고 느끼지 않고, 기하 문제라고 꺼리지 않는 Competitive Programmer가 되었으면 합니다.
1. 도형의 기본 구성 요소
기하 구현이 까다로운 이유 중 하나는 직선을 표현하는 방법이 많다는 것과 동시에 그 선택이 코딩 난이도에 큰 영향을 준다는 것입니다. 예를 들어, $y=ax + b$ ($a$, $b$는 변수)의 형태로 직선을 표현하는 경우 수직선을 표현하기 어렵습니다. 수직선을 일반적인 직선과 따로 처리한다면 예외 처리가 너무 많아져 쉬운 문제를 어렵게 풀거나 어려운 문제에서 풀이를 알아도 코딩에 실패할 수 있습니다.
여기서는 기본 구성 요소를 표현하는 서로 다른 많은 방법과 각각의 장단점을 다룹니다.
1) 점
점은 (x좌표 값, y좌표 값)으로 표현하는 것이 최선입니다. 가끔 다른 표현법이 더 좋은 경우가 있지만, 코딩이나 풀이에 대한 이점이 크지 않아 고민하지 않아도 됩니다.
참고) Homogeneous coordinate로 점을 표현하는 방법도 있지만, 사영 기하에 대해 정확하게 아는 것이 아니라면 이점이 거의 없습니다.
코드는 한 구조체/클래스 안에 변수 2개를 선언하는 형태가 가장 좋습니다. x좌표와 y좌표가 구조체나 클래스로 묶여있지 않으면 코드가 더러워질 가능성이 높아집니다. 방법은 많이 있으니 가장 마음에 드는 것을 쓰시면 됩니다.
struct Point{
int x, y;
};typedef std::pair<int, int> Point;혹은, 틀리지 않을 자신이 있다면
typedef complex<long long> Point;
하지만 좌표값의 자료형은 선택이 필요합니다. int, double, 분수를 정의해서 쓰거나, 더 가면 (저는 해보지 않았지만) $a+b\sqrt{c}$같은 특이한 자료형을 정의해서 쓸 수도 있습니다.
(1) 정수 자료형
모든 기하 문제는 정수만 써서 해결한다는 생각을 가지고 있는 것이 좋습니다. 정수는 오버플로우만 올바르게 확인했다면 우리를 배신하지 않습니다. 코딩이 과하게 어려워지는 경우가 아니라면 분수를 써서라도 정수 자료형으로만 문제를 해결하는 것을 추천드리고, 기하 문제를 풀 때는 정수 자료형만으로 해결 가능한지 확인하는 습관을 들이는 것이 좋습니다. 간혹 long long 자료형을 벗어나는 경우가 있지만 우리에게는 __int128이 있으니 꼭 정수를 쓰도록 합시다.
실수 자료형을 관리하는 방법은, 저도 정확히 모르고, 그 내용도 매우 방대하여 여기서 심도있게 다룰 수 있는 내용은 아닌 것 같습니다. 여기서는 실수 자료형을 회피하는 방법 몇 가지만 설명해 드리겠습니다.
보통 기하 문제는 정확한 값 보다는 크기 비교가 중요한 경우가 많습니다. 예를 들어, $(2, 2)$가 원점을 중심으로 하는 반지름 $3$인 원 내부에 있는지는 원점과 $(2, 2)$의 거리를 정확하게 계산하지 않아도 알 수 있습니다. ($2^2+2^2 = 8 < 9$)
(2) 실수 자료형
정수 자료형으로 대부분의 문제를 해결할 수 있지만, 반대로 해결할 수 없는 경우도 가끔 나옵니다. 루트가 등장하는 경우가 있고, 분수에 적용되는 사칙연산이 너무 많아 분모/분자에 overflow가 나는 경우도 있습니다. 물론 그 외에 더 있을 수 있고, 그때마다 정수만 사용할 수 있는지 진지하게 고민해 봐야 합니다.
실수 자료형을 쓰기 전에 일단 실수 자료형이 어떻게 생겼는지 알아볼 필요가 있습니다. double은 실수를 64bit으로 저장합니다. 하지만 모든 실수를 겨우 64bit에 담는 것은 불가능하기 때문에, 컴퓨터는 특정한 $2^{64}$개의 실수를 골라 저장합니다. 만약 $2^{64}$개 중에 그 수가 없다면 가장 가까운 수를 대신 저장합니다.
$2^{64}$개의 값은 대략 아래처럼 생겼습니다.

double 기준, 그림에서 1과 2 사이에 $2^{53}$개(약 $8 \times 10^{15}$)의 수가 있습니다. 따라서 1과 $1+10^{-18}$은 double 자료형에서 같은 값으로 대응됩니다. 이런 이유에서 실수 자료형에 크기 차이가 매우 많이 나는 (거의 $10^{15}$배 차이나는) 값을 더하거나 빼는 것은 위험합니다. 약간의 응용을 하면, 크기 차이가 매우 작은 (차이가 원 값의 $10^{-15}$배정도 되는) 두 값을 빼는 것도 위험합니다.
이론적인 부분은 위와 같지만, 실제로 실수 오차를 정밀하게 확인하면서 코딩하는 것은 매우 어렵습니다. 그래서 차이가 ($10^{-18}$ 정도로) 매우 작은 두 변수의 비교 결과가 답에 큰 영향을 미치는 경우에는 실수를 쓰면 안 됩니다.
대표적인 예시가 https://www.acmicpc.net/problem/13315이니, 한 번 풀어보시면 좋습니다. 20년도 SCPC 본선 4번 또한 마지막 단계가 아닌 부분에서 실수 자료형을 쓰면 틀리는 문제인데, 난이도가 꽤 높으니 참고해서 보시기 바랍니다. 출제자 코멘트로 기울기의 정확도가 $10^{-30}$정도여야 해서 기울기로 실수 자료형을 쓰면 무조건 틀린다고 합니다.
(3) 분수, 루트, …
모든 커스텀 자료형은 실수를 쓰지 않으려고 씁니다. 분수를 제외하고는 써본 적이 없지만, 기하가 아닌 다른 문제에서는 사용해야 할 수도 있습니다.
2) 벡터

벡터는 고등학교 수준에 해당되는 내용이고, 수능에도 빠지는 추세지만, 기하 문제를 풀기 위해서는 알아두는 것이 좋습니다. 벡터는 “두 점의 상대적 위치”를 나타내는 값이기 때문에 기하 문제를 풀 때 자주 사용됩니다.
벡터는 회전시킬 수는 없지만, 평행 이동은 가능한 화살표라고 생각하면 편합니다.
두 수에 사칙연산을 할 수 있는 것처럼, 두 벡터에도 사칙연산과 비슷한 연산이 있습니다. 이 연산에는 덧셈, 뺄셈과, 곱셈과 나눗셈에 대응되는 연산인 외적과 내적이 있습니다. 특히 외적은 CCW로 잘 알려져 있는 시계방향 확인에 필요하여 자주 쓰입니다.
외적 및 내적은 인터넷이 자료가 많이 있어 자세히 다루지는 않으려 합니다. 대신 약간의 자료를 아래 첨부합니다.
참고. 두 2차원 벡터는 외적이 정의되어 있지 않지만, 두 2차원 벡터 $(x_1, y_1)$과 $(x_2, y_2)$의 외적을 CCW 값인 $x_1y_2 - x_2y_1$으로 정의해서 쓸 수 있습니다.
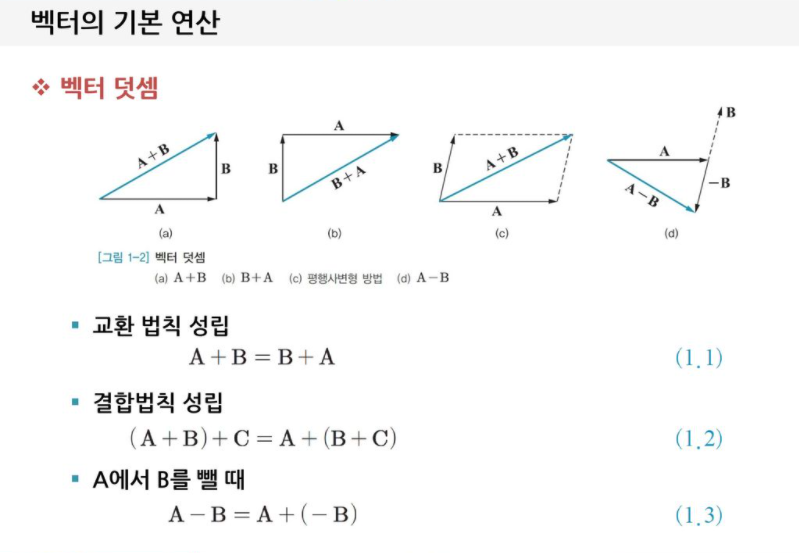

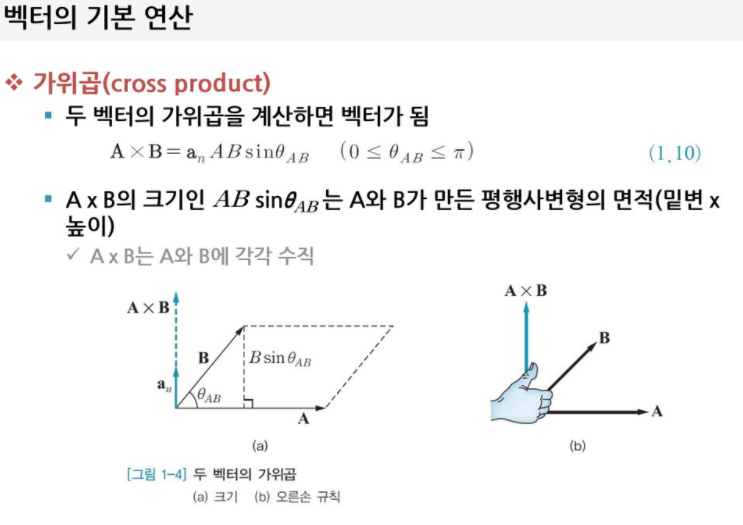
(출처: https://slidesplayer.org/slide/11219604/)
저는 아래와 같이 operator를 재정의하여 사용합니다. (*은 내적, /은 외적입니다)
pii operator + (pii l, pii r){ return pii(l.first + r.first, l.second + r.second); }
pii operator - (pii l, pii r){ return pii(l.first - r.first, l.second - r.second); }
ll operator * (pii l, pii r){ return (ll)l.first * r.first + (ll)l.second * r.second; }
ll operator / (pii l, pii r){ return (ll)l.first * r.second - (ll)l.second * r.second); }
3) 직선, 선분
직선은 기하 문제에서 가장 많이 나오는 구성 요소입니다. 직선을 저장하는 방법이 많기 때문에 직선을 올바르게 표현하는 방법만 익혀도 기하 문제 코딩이 한결 쉬워질 것입니다. 선분 또한 직선에 범위만 지정한 형태로 사용하기 때문에 직선과 비슷합니다.
(1) $y = ax + b$
직선을 “기울기”와 “y절편의 값”으로 나타내는 방법입니다. 주로 DP최적화나 Convex Hull Trick과 같이 정수 기울기만 등장하는 경우나, 일부 기하 문제에서도 사용됩니다. 이 형태의 표현법은 매우 직관적이고 다루기 편하지만, 수직선이 등장하기 시작하면 예외 처리의 지옥이 펼쳐집니다. 또한 유리수 기울기가 가능한 경우 분수를 구현해야 해서 코딩이 길어지는 단점이 있습니다.
+ 쓸 수만 있다면 가장 좋은 형태이다.
- 쓸 수 있는 상황이 매우 한정적이다.
(2) $ax + by + c = 0$
보통은 직선이 나오는 문제를 풀어야 하는데 수직선이 등장하거나 유리수 기울기가 가능한 경우 $y = ax + b$는 못써서 $ax + by + c = 0$을 쓰는 경우가 많습니다. 그 외에도 Homogeneous coordinate에서 사용되는 직선 형태입니다.
저는 개인적으로 이 형태를 매우 싫어합니다. 먼저 특정 기울기를 가지는 어떤 점을 지나는 직선을 만들려면 식을 좀 써야 합니다. 선분을 표현하는 방법도 만만치 않고, 원과의 교점을 구하는 것도 어렵고, 그 외에도 귀찮은 점이 많습니다. 개인적으로 (1) 번 형태를 쓸 수 없는 상황이면 아래 형태를 쓰는 것이 더 좋다고 생각합니다.
- 다루기 어렵고 코딩이 복잡하다.
(3) $\vec{u} + k\vec{v}$
직선 위의 한 점 $\vec{u}$와 직선의 방향벡터 $\vec{v}$, 그리고 실수 파라미터 k를 이용하여 직선을 나타내는 방법입니다. 직선 위의 점과 실수 k가 일대일 대응이 된다는 것이 특징입니다. (편의상 점을 원점으로부터의 벡터로 표현합니다. 수학과가 보면 분노하겠지만, 점과 벡터를 같은 구조체로 코딩하는 것이 더 짧고 간단합니다)
끝 점이 A와 B인 선분을 표현할 때는, $\vec{A} + (\vec{B}-\vec{A})k$ (단, $0 \le k \le 1$)로 간단하게 표현할 수 있습니다.
기본적으로 점과 벡터를 이용한 표현법이기 때문에, 외적이나 내적과 같은 벡터 연산에 익숙하지 않으면 다루기 어렵습니다. 하지만 기초를 다질 수만 있다면 편하게 쓸 수 있습니다. 벡터를 잘 몰라도, 모든 것을 수식으로 계산할 수 있는 능력이 되면 나쁜 표현법은 아닙니다.
+ 예외 없이 모든 직선과 선분을 표현할 수 있다.
- 외적 및 내적에 대한 이해가 없다면 다루기 어렵다.
2. 예외 처리
기하는 예외 처리의 분야입니다. 기하 문제에는 예외 처리가 필요한 경우가 많습니다. 보통 한 가지 방법으로 모든 경우가 해결되는 경우는 거의 없고, 적으면 두세 가지 방법으로, 많으면 열 가지가 넘는 경우를 나눠서 처리해야 하는 경우도 있습니다. 대신 예외 처리를 해야 하는 조건은 어떤 기하 문제가 나와도 비슷하다는 특징이 있습니다. 기하 문제에 공통으로 등장하는 예외 처리 조건들을 외우고 있으면 경우를 나누는 데 큰 어려움이 없을 것이라 생각합니다.
기하 문제에서 자주 등장하는 예외 처리 조건들입니다.
- (입력 혹은 Convex hull처럼 전처리 후 남은) 점이 1개
- (입력 혹은 Convex hull처럼 전처리 후 남은) 점이 일직선
- 점이 2개
- 세 점이 일직선
- 직선/선분이 평행
- 직선/선분이 일직선 위에 존재
- 점이 선분/직선/원 위에 있음
예외처리가 적당히 필요한 문제들을 가지고 실제 기하에서 예외 처리가 어떤 식으로 이뤄지는지 보려고 합니다.
1) 선분과 선분 교차
많은 기하 문제에서 등장하지만, 동시에 예외가 매우 많이 등장하는 문제입니다. 두 선분을 $\vec{u} + k\vec{v}$, $\vec{x} + l\vec{y}$라 하겠습니다.
(1) 두 선분이 평행하지 않은 경우
평행하지 않은 경우 판별은 두 방향벡터의 외적 값인 $\vec{v} \times \vec{y} \neq 0$인지 확인하면 됩니다.
가장 잘 알려진 방법부터 언급하겠습니다. CCW 4번으로도 가능하고, 가장 많이 알려진 방법이라고 생각합니다. 대신 저에게는 예외 처리가 직관적이지 않아 다른 방법을 쓰고 있습니다. 선분의 한쪽 끝이 반대쪽 선분 위에 올라가는 예외상황을 잘 처리할 수 있으면 상관이 없습니다. 추가로 CCW 2개를 곱할 때 integer overflow가 나지 않도록 주의해주세요.
저는 다음과 같은 방법을 선호합니다. 먼저 직선으로 가정하고 식을 세워보면 $\vec{u} + k\vec{v} = \vec{x} + l\vec{y}$인 실수 $k$, $l$을 구하는 문제가 됩니다. 수식을 정리하고 연립방정식으로 풀어도 됩니다. 저는 양 변에 $\vec{v}$를 외적 해서 $l$을, $\vec{y}$를 외적해서 $k$를 구합니다. 식을 정리해 보면 다음과 같이 됩니다. (외적을 할 때, 순서에 주의해서 해야 합니다.)
$(\vec{u} + k\vec{v}) \times \vec{v} = (\vec{x} + l\vec{y}) \times \vec{v}$
$(\vec{u} - \vec{x}) \times \vec{v} = (\vec{y} \times \vec{v})l$
$l = ((\vec{u} - \vec{x}) \times \vec{v}) / (\vec{y} \times \vec{v})$
마찬가지로, $k = ((\vec{x} - \vec{u}) \times \vec{y}) / (\vec{v} \times \vec{y})$
위에서 구한 $k$와 $l$이 모두 0 이상 1 이하여야 하다는 것을 가지고 확인하면 됩니다. 선분 위에 끝점이 있다거나 하는 이상한 경우도 $k$와 $l$의 값에 들어가는 부등호에 등호가 들어가는지 들어가지 않는지 선택하는 것으로 처리할 수 있습니다.
- 참고. $a / b < 1$을 확인할 때 $b$가 음수일 수 있는 경우 양 변에 $b$를 곱해서 $a < b$를 확인하면 안 됩니다. 때문에 분수를 코딩할 경우 분모가 항상 양수가 되도록 하는 것이 좋습니다.
(2) 두 선분이 평행하지만, 일직선 위에 있지 않은 경우
선분 위의 두 점을 이은 직선이 선분과 평행하지 않다는 것으로 확인할 수 있습니다. 이는 아래 식으로 확인할 수 있습니다.
$(\vec{u}-\vec{x}) \times \vec{v} \neq 0$
(3) 두 선분이 평행하고, 일직선 위에 있는 경우
보통 자주 쓰는 방법은 두 선분의 Bounding Box가 겹치는지 확인하는 방법을 사용합니다. 저는 선분의 양쪽 끝이 포함되는지 여부 처리가 까다로워서 잘 안 쓰지만, 일반적인 경우에는 bounding box로 해결해도 문제는 없을 것입니다.
이 경우는 하나의 직선 위에 구간이 2개 있는 경우로 바꿔 생각할 수 있습니다. 두 선분을 수평선 위의 값 하나로 매핑을 해야 하는데, 저는 $\vec{u}$를 0으로, $\vec{u} + \vec{v}$를 $\vec{v} \cdot \vec{v}$로, $\vec{x}$를 $(\vec{x}-\vec{u}) \cdot \vec{v}$로, $\vec{x}+\vec{y}$를 $(\vec{x}+\vec{y}-\vec{u}) \cdot \vec{v}$로 매핑해서 사용합니다. 이제 $[0,\vec{v} \cdot \vec{v}]$과 $[(\vec{x}-\vec{u}) \cdot \vec{v}, (\vec{x}+\vec{y}-\vec{u}) \cdot \vec{v}]$ 구간이 겹치는 지 여부로 확인하면 됩니다. (참고: 평행한 두 벡터에 대한 내적은 두 벡터의 길이의 곱이 됩니다.)
오랫동안 고민해봤지만, 두 선분이 교차하는지 여부는 적어도 3가지 경우를 확인해야 하는 것 같습니다.
2) Convex Hull
Convex Hull을 구하는 방법은 여기서 자세하게 다루지는 않을 것입니다. 방법을 간략하게 설명하자면,
- y좌표가 가장 작은 점을, 여러 개가 있다면 x좌표가 가장 작은 점을 고릅니다.
- 그 점을 원점으로 하여 각도 정렬을, 각도가 같다면 거리 순서로 정렬합니다.
- 정렬된 순서대로 스택에 점을 넣는데, 넣기 전에 넣으려는 점과 스택 위의 점 2개의 CCW를 확인하여 조건을 만족하면 뺍니다.
Convex Hull이 겉보기에는 가장 기초적인 알고리즘이지만, 특정 상황이 되면 생각하지 못한 예외가 많이 발생하는 알고리즘입니다. 특히 점이 겹치는 경우가 처리하기 매우 까다롭습니다.
(1) 모든 점이 다르고, Convex Hull 위의 세 점이 한 직선 위에 있지 않은 경우
이 경우는 기존 방법대로 하면 문제가 없습니다.
(2) 모든 점이 다르고, Convex Hull이 세 점이 한 직선인 경우를 포함시켜야 하는 경우
기존 방법대로 하면 Convex Hull의 마지막 부분에서 문제가 생길 수 있습니다. 각도가 가장 큰 점이 여러 개인 경우 예외가 생길 수 있습니다. 그림에서 BCDE 순서로 점을 추가하는데, D를 추가할 때 C를 제거하고, D를 추가할 때 E를 제거하기 때문에 C와 D가 Convex Hull에 포함되지 않습니다.

가능한 방법으로 각도가 가장 큰 점들의 순서를 뒤집은 뒤 기존 Convex Hull 알고리즘을 따라가는 것이 있습니다.
(3) 같은 점이 가능한 경우
같은 점을 모두 없앨 수 있다면 가장 좋겠지만, 간혹 그럴 수 없는 경우가 존재합니다. 이 경우 신중히 예외 처리 경우들을 고려해야 틀리지 않을 수 있습니다.
먼저 원점에 점이 2개 이상 있는 경우를 조심해야 합니다. 정렬해야 하는 배열에 원점이 있으면 각도 정렬이 안됩니다. 때문에 각도 비교를 하기 전에 원점인지 여부를 확인하거나, 미리 원점을 앞으로 빼서 처리하는 것이 좋습니다.
점을 순서대로 처리할 때도 조심해야 합니다. 스택에 같은 점이 2개 이상 들어간 경우, 다음 점은 무조건 일직선 위에 있는 것으로 판단하게 됩니다. 때문에 스택에 같은 점이 들어가지 않도록 조심해야 합니다.
저는 이 경우 다음과 같은 구조체를 선언하여 Convex Hull을 구합니다. 같은 점이 연달아 들어오는 경우 스택에 점을 추가하는 대신, 스택의 마지막 원소에 있는 vector에 점을 추가합니다.
struct{
Point p;
vector<int> index;
}
3) 360도 각도 정렬
360도 각도 정렬은 경우의 수가 많다고 느껴질 수 있지만, 사실 별로 없습니다. 180도보다 작은 각도 2개는 CCW로 비교할 수 있기 때문에 비교 대상인 두 점이 모두 1, 4 사분면이나 2, 3 사분면에 위치하면 CCW로 비교하고, 아닌 경우 1, 4 사분면에 있는 점이 더 크다고 판별하면 됩니다.
코드는 아래와 같습니다. (O는 원점입니다)
sort(P, P+N, [](pii l, pii r){ return (l < O) != (r < O) ? l < r : l/r > 0; });
4) 선분과 원 교차
직선과 원의 교점은 직선 위의 점들 중 원의 중심 O와의 거리가 r인 점을 찾는 문제가 됩니다. 직선을 $\vec{u} + k\vec{v}$라 하면 다음과 같은 식을 세울 수 있습니다.
$|| \vec{u} + k\vec{v} - \vec{O} ||^2 = r^2$
이 식을 내적을 써서 전개하면 다음과 같이 됩니다.
$(\vec{u} + k\vec{v} - \vec{O}) \cdot (\vec{u} + k\vec{v} - \vec{O}) = (\vec{v} \cdot \vec{v})k^2 + 2(\vec{u}-\vec{O}) \cdot \vec{v}k + (\vec{u}-\vec{O}) \cdot (\vec{u}-\vec{O}) = r^2$
위 식은 $k$에 대한 2차식이라서 $k$를 구할 수 있습니다.
(1) 해가 0개인 경우는 직선과 원이 만나지 않습니다.
(2) 해가 1개인 경우는 직선과 원이 접합니다.
(3) 해가 2개인 경우는 직선과 원이 두 점에서 만납니다.
교점이 선분 위에 있는지의 여부는, $k$가 0 이상 1 이하인지 확인하면 됩니다.
5) 다각형과 직선
다각형에서 반직선이나 직선을 그어 교점을 구하는 문제는 많이 있습니다. 점이 다각형 내부에 존재하는지 여부를 구하는 것이 대표적인 예시입니다. 반직선을 우리가 결정할 수 있는지 여부는 이런 종류의 문제에서 꽤 중요하게 작용하게 됩니다.
(1) 직선이 정해져 있지 않는 경우
직선을 아무렇게나 그어도 된다면, 직선이 다각형의 꼭짓점을 지나지 않도록 X축과 거의 평행한 선분을 긋거나, 랜덤하게 그어본 뒤 꼭지점을 지나면 다시 그어보는 방법을 택하면 됩니다. 되도록이면 직선이 다각형의 꼭지점을 지나지 않도록 해야 예외 처리로 고통받지 않을 수 있습니다.
(2) 반직선이 정해진 경우
간혹 반직선을 아무렇게나 그을 수 없는 경우가 가끔 등장하고, 이 경우는 경우를 자세하게 나눌 필요가 있습니다. 예시로는 https://www.acmicpc.net/problem/14633 나, https://www.acmicpc.net/problem/16683 가 있습니다.
이 경우가 복잡한 이유는, 직선과 다각형의 변이 겹치거나, 직선이 꼭지점을 지나는 등의 예외가 매우 많아 틀리기 쉽고, 예외를 처리하는 쉬운 방법이 딱히 없습니다. 또한 선분 교차가 들어가는 만큼 실수 자료형을 쓰기 쉽고, 여기서 실수 오차가 발생할 수도 있습니다. 때문에 이런 예외는 피할 수 있으면 피해야만 합니다.
완벽하게 일반화시킨 코드는 MolaMola 팀노트 22페이지에 있습니다. 코드 결과물만 설명하자면, 꼭짓점이 반시계 방향으로 저장된 다각형 $C$와 점 $\vec{A}$, 방향 $\vec{d}$를 인자로 받아, $\vec{A}+k\vec{d}$ 직선에 대해 $k$가 작은 값부터 순서대로 다각형과의 접촉 이벤트와 그때의 k값을 $R$에 저장하는 코드입니다. (이유는 잊어먹었지만, d의 x 성분과 y 성분은 서로 소여야 합니다.) 이벤트는 0번부터 7번까지 8개의 이벤트가 있는데, 순서대로 다음과 같습니다.
0. 다각형의 밖에서 다각형의 선분 위로 이동
1. 다각형의 안에서 다각형의 선분 위로 이동
2. 다각형의 선분 위에서 다각형의 밖으로 이동
3. 다각형의 선분 위에서 다각형의 안으로 이동
4. 다각형의 꼭짓점을 밖에서 지남
5. 다각형의 꼭지점을 안에서 지남
6. 다각형의 밖에서 안으로 이동
7. 다각형의 안에서 밖으로 이동
물론 실제로 모든 이벤트를 다 구별해야 하는 문제는 아직까지 보지 못했습니다. 때문에 이 정도까지 복잡한 코드는 일반적으로 필요가 없습니다만, 월파 준비하던 시절에는 무슨 문제가 나올지 몰라 준비한 코드입니다.
추신. 팀노트에 그림을 넣어놨는데, 지금 보니 조금 틀렸네요. 앞에서 2번째, 3번째, 7번째 화살표에 대한 다각형 영역이 반대로 그려져 있습니다. 참고로, 다각형의 꼭짓점을 반시계 방향으로 저장했다면 i와 i+1번째를 잇는 벡터의 왼쪽이 다각형의 영역이 됩니다.

+ 간단하게 방법을 설명하자면, 먼저 직선과 다각형의 교점을 모두 구한 뒤, 선분의 $k$값 순서대로 이벤트를 만들어 나가는 코드입니다.
3. 기하 문제의 특징
기하 문제는 전수 조사가 안 되는 경우가 많습니다. "가능한 모든 도형에 대해 최솟값을 구하여라"라는 문제 세팅에서는 가능한 도형의 가짓수가 무한히 많아 전수조사를 할 수 없습니다. 이것은 도형의 가짓수가 이산적이지 않고 연속적이기 때문에 발생하는 일입니다.
다음과 같은 문제를 생각해 봅시다.
“점 N개가 주어져 있다. 평행한 두 선을 그어 모든 점이 두 선 사이에 위치하도록 하되, 두 선의 거리가 최소가 되도록 하고 싶다. 두 선의 거리를 구하여라.”
이런 문제들은 중요한 값을 조금 바꿔도 변하지 않는 특징을 찾는 것이 문제 해결에 도움이 됩니다. 이 문제에서는 기울기를 조금은 바꿔도 변하지 않는 특징을 한번 생각해 보는 것입니다. 아래 그림을 보면 기울기가 바뀐 상황에도 빨간 직선은 점 P6을, 파란 직선은 점 P5를 지나는 것을 볼 수 있습니다.

여기서 생각을 조금 더 발전시키면, 가능한 기울기는 많아도 두 직선이 지나는 점의 쌍은 유한하다는 것으로 경우를 나눌 수 있습니다. 더 가면, 점의 쌍 하나에 대해 풀면 전체 문제 또한 해결할 수 있다는 풀이가 가능합니다. 점의 쌍을 (A, B)라 하고 한 직선은 점 A를, 다른 직선은 점 B를 지나야 한다고 가정하고, 기울기 범위를 찾고, 그 범위 내에서는 수식을 정리하여 O(1)에 최솟값을 계산하는 풀이법을 고려해볼 수 있습니다.
모든 것을 한 곳에 모으면 다음과 같은 풀이가 완성됩니다.
+ 모든 두 점 (A, B)에 대해, 한 직선은 A를, 다른 직선은 B를 지나는 기울기 범위를 계산하고, 그 범위에서 기울기의 최솟값과 최댓값일 때 두 직선의 간격을 구하여 최솟값을 계산한다.
4. 후기
지금까지 기하 문제를 풀어오면서 고민했던 내용을 정리해 보았습니다. 글 도입부에서 말했듯, 기하 문제가 더 이상 장애물이 되지 않으면서, 동시에 많은 자료가 많은 분들의 블로그에서 만들어졌으면 합니다. 그리고 틀린 점이나 질문, 추가하거나 설명했으면 하는 내용을 알려주시면 지속적으로 추가하려고 합니다.
끝!
'ICPC, CP 칼럼' 카테고리의 다른 글
| 지구이의 프로그래밍 스터디 그룹 개설 (2) | 2021.06.10 |
|---|---|
| UCPC 2020 본선 후기 (1) | 2020.08.04 |
| Voronoi Diagram O(N log N) 구현 (1) | 2019.12.07 |
| 분수 이진탐색과 Stern–Brocot tree (0) | 2019.03.12 |
| == UCPC F. parentheses recover 풀이 == (feat. 모델링의 중요성) (0) | 2018.11.14 |
